


$\displaystyle e = \frac \, dx$įor the master list of symbols, see mathematical symbols. The following table documents some of the most notable symbols in these categories - along with each symbol’s example and meaning. In calculus and analysis, constants and variables are often reserved for key mathematical numbers and arbitrarily small quantities. $$ \to ∫f(X')d(x'_1)∧.∧d(x'_n)= ∫f((ϕ(X)) \detd(x_1)∧.∧d(x_n)$$Īs a true Frenchman Cartan quickly axiomatized and generalized his powerful invention, and left future generations wondering what the Hell's going on.Yes.

If your coordinates are $(x_1,\cdots,x_n)$ and your vector expressed in Euclidean coordinates at a point $x$ is $v=(v_1,\cdots,v_n)$, we can write the vector as an object of the form I defined above by writing $$v=v_1\frac$$ But if you like coordinates, do not worry we can transfer between these two definitions. But the problem with that is that those coordinates depend on the coordinate system we choose to use. What does this mean, and how does it relate to vectors as we are used to seeing them? We are used to seeing vectors defined by a collection of components. Where $f$ and $g$ are smooth functions on $M$ and $\lambda$ is a real number (notice something that looks like the product rule). A vector $v$ at a point $x$ in a smooth manifold $M$ is any function whose domain is $C^\infty(M)$ and whose range is $\mathbb R$, and which satisfies the following three properties: This definition is probably going to sound really strange, but it really is the simplest way to define vectors on smooth manifolds. In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. Now we will talk about a vector at a point on a smooth manifold. If things are moving a little fast for you, you may some up the last three paragraphs as, "we have spaces that up close look like Euclidean space, and functions on them that are in some sense differentiable." The set of all smooth functions on a manifold $M$ is called $C^\infty(M)$ More complex examples are varied and interesting, but are difficult to define in an informal setting.Ī smooth manifold is a manifold where the Euclidean regions around each point are in some sense "compatible." This means that if the Euclidean regions of two points overlap, I can both Euclidean coordinate systems in that overlap region, and transfer from one to the other in an infinitely differentiable way.Ī smooth function on a smooth manifold is a function whose range is the real numbers, and which is infinitely differentiable with respect Euclidean coordinate systems in the Euclidean regions around points in the manifold. That is, the area around every point in a manifold "looks like" Euclidean space, but the space as a whole may not be Euclidean. Who Invented Calculus Calculus was developed in the latter half of the 17th century by two mathematicians, Gottfried Leibniz and Isaac Newton.
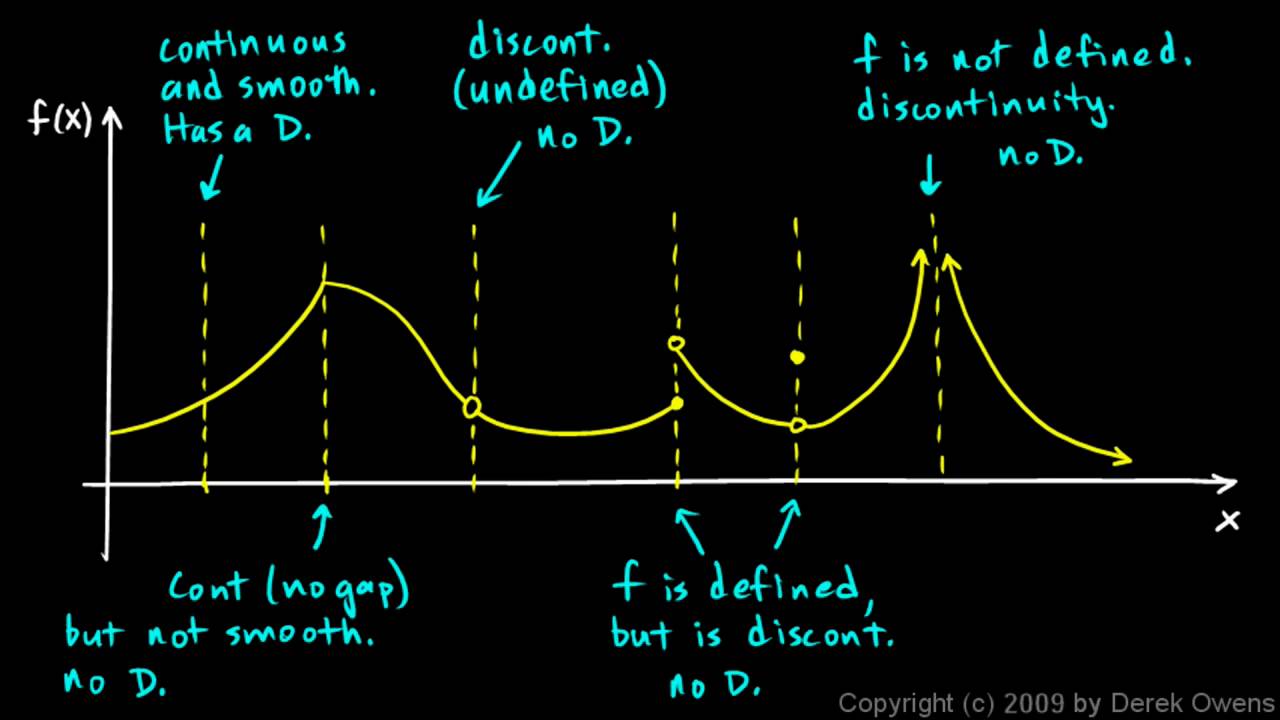
Informally speaking, a manifold is any space which is locally Euclidean. There are two types of calculus: Differential calculus determines the rate of change of a quantity, while integral calculus finds the quantity where the rate of change is known. To talk about differential forms, first we need to talk about manifolds and vector fields.


 0 kommentar(er)
0 kommentar(er)
